Implementierung des Vigenère Solvers
Übersicht
Ich stelle auf dieser Seite ein Verfahren sowie die entsprechende Implementierung in PHP vor, um Vigenère-Cipher mit Hilfe von Bigrammen ohne Kenntnis des Schlüssels zu lösen. Die hier vorgestellten Ansätze sind in diesem Online Vigenère-Solver umgesetzt.
Der Vigenère-Cipher - der Klassiker unter den Verschlüsselungsmethoden
Oftmals wird die Erfindung dieser polyalphabetischen Verschlüsselung Blaise Vigenère zugeschrieben. Dies ist laut einigen Quellen wohl nicht korrekt, wie ein Blick zu Wikipedia zeigt. Erfunden hat Blaise Vigenère diesen Cipher nicht, aber auf ihn geht eine Variante dieses Codes, der Autokey Cipher, zurück. Trotz dieser Namensgeberverwirrung werde ich zum Vigenère-Cipher weiterhin "Vigenère-Cipher" sagen.
Was treibt mich dazu, mich mit diesem Code zu beschäftigen? Ganz einfach, er wird in vielen Geocaching Rätseln verwendet. Zudem ist dieser Code hervorragend geeignet, sich mit den Grundprinzipien der Verschlüsselung bzw. der Entschlüsselung auseinander zu setzen.
Wie dieser Cipher funktioniert, wird ausführlichst an anderen Stellen im Internet beschrieben. Das ist gut so, denn so kann ich hier etwas anderes darlegen, nämlich, wie man einen Vigenère-Cipher ohne Kenntnis des Schlüssels dekodieren kann.
Das ist nichts neues, gibt es doch eine Reihe von Online Vigenère-Solvern im Netz. Diese Solver funktionieren auch recht gut, solange der verschlüsselte Text sehr viel länger ist als der Schlüssel. Wird aber der Text im Verhältnis zum Schlüssel immer kürzer, so ändert sich das Bild. Leicht kommt es vor, dass in solchen Fällen die Schlüssellänge nicht korrekt bestimmt wird, und selbst bei korrekter Schlüssellänge weicht oftmals der bestimmte Schlüssel so stark von der richtigen Lösung ab, dass der Text letztlich nicht oder nur mit zusätzlicher mühevoller Handarbeit entschlüsselt werden kann.
Typische Funktionsweise von Vigenère-Solvern
Die meisten Vigenère-Solver arbeiten nach dem gleichen Prinzip. Zuerst wird mit Hilfe einer Autokorrelation die Schlüssellänge bestimmt. Eventuell kommt dafür auch der Friedman-Test zum Einsatz.
Ist die Schlüssellänge bestimmt (z.B. n=7), reduziert sich die polyalphabetische Verschlüsselung auf z.B. n=7 monoalpabetische Verschlüsselungen. Dazu werden die Buchstaben des verschlüsselten Textes in n=7 Gruppen aufgeteilt. Der erste, der achte, der 15. usw. Buchstabe kommen in die erste Gruppe, der zweite, neunte, 16, usw. Buchstabe in die zweite Gruppe und so weiter. Nun wird mit Hilfe einer Buchstabenhäufigkeitsverteilung jede Gruppe einzeln betrachtet. Ist z.B. in der dritten Gruppe der Buchstabe "G" am häufigsten vorhanden, entspricht er aller Wahrscheinlichkeit nach im Klartext dem "E". Mit Hilfe des Vigenère-Quadrats kann somit der Buchstabe des Schlüssels bestimmt werden. In diesem Beispiel würde der dritte Buchstabe des Schlüssels "C" heißen, denn der Schlüsselbuchstabe "C" verschlüsselt den Buchstaben "E" zu "G".
Dieser Ansatz hat zwei Schwachpunkte, die beide zum Tragen kommen, wenn der Ciphertext im Verhältnis zum Schlüssel recht kurz ist.
Zum einen liefern sowohl die Autokorrelation als auch der Friedman-Test keine zuverlässigen Ergebnisse mehr. Die Suche nach der richtigen Länge des Schlüssels kann leicht zu einer Raterei werden.
Zum anderen wird jede Gruppe für sich alleinstehend betrachtet. Die Analyse findet damit auf Basis eines Monogramms (also eines einzelnen Buchstabens) statt. Befinden sich sehr wenige Buchstaben in einer Gruppe, wird eine statistische Auswertung sehr ungenau. Leicht ist ein Buchstabe des Schlüssels falsch bestimmt, was schnell dazu führt, dass der daraus resultierende Klartext nicht mehr als solcher erkannt werden kann.
Der Ansatz: Bigramme
Der Vigenère-Cipher wird gebrochen, indem unterschiedliche Schlüssel ausprobiert werden. Zu jedem Schlüssel wird der Klartext gebildet, und je ähnlicher der Klartext der vorgegebenen Sprache kommt, desto wahrscheinlicher handelt es sich um den richtigen Schlüssel. Wir brauchen also ein Verfahren, das einen Klartext entsprechend bewerten kann. Dazu wird der Begriff der "Fitness" eingeführt. Zu jedem Klartext wird seine Fitness bestimmt. Die Fitness eines Textes ist ein Zahlenwert, je größer dieser Wert ist, desto näher kommt der Text der vorgegebenen Sprache.
Es gibt unterschiedliche Verfahren, um einen Text so zu bewerten. Das hier verwendete Verfahren basiert auf der Analyse mittels Bigrammen und ihrer Häufigkeiten.
Was genau ist ein Bigramm? Der Text "Vigenere" besteht aus acht Buchstaben (Monogrammen) und damit aus sieben Bigrammen, nämlich "vi", "ig", "ge", "en", "ne", "er" und "re". Statt eine Häufigkeitsanalyse auf der Basis einzelner Buchstaben durchzuführen, wird die Häufigkeit von aufeinander folgenden Buchstabenpaaren betrachtet. Das häufigste deutsche Bigramm lautet "ER" (3,9%), im Englischen hingegen ist "TH" (2,7%) das am häufigsten verwendete Buchstabenpaar.
Die Bigrammanalyse ist also von der verwendeten Sprache abhängig. Das gilt übrigens auch schon für die Häufigkeitsanalyse einzelner Buchstaben (Monogramme). Für den Vigenère-Solver bedeutet das, dass die zu erwartende Sprache des Klartextes vorgegebenen werden muss, damit die entsprechende Häufigkeitstabelle verwendet werden kann.
Im folgenden werden wir uns auf die deutsche Sprache konzentrieren.
Die Analyse eines Klartextes basierend auf Bigrammen liefert eine zuverlässigere Aussage als eine entsprechende Analyse basierend auf Monogrammen. Die Frage, die sich damit stellt: Wenn Bigramme bessere Ergebnisse als Monogramme liefern, wie sieht es dann mit Trigrammen aus? Antwort: Noch besser. Und mit Quadgrammen? Noch noch besser.
Man spricht im allgemeinen von N-Grammen, aber im folgenden werden wir uns auf Bigramme beschränken (d.h. N=2). Zu N-Grammen nur noch so viel: N beliebig weiter zu erhöhen hat seine Grenzen. Erst einmal natürlich steigen die Anforderungen an die Rechner-Resourcen, aber auch die Güte des Ergebnisses verkehrt sich ins sehr schnell ins Gegenteil. So sollen Quintgramme (5-Gramme) schlechtere Ergebnisse liefern als Quadgramme.
Neue Frage: Wo bekommen wir die Bigramme und ihre Häufigkeiten für die deutsche Sprache her? Eine gute Seite, die ich gefunden habe, ist practicalcryptography.com. Dort gibt es N-Gramme für die unterschiedlichsten Sprachen, darunter auch für Deutsch.
Die Datei german_bigrams.txt ist erstellt worden, indem von einem sehr langen deutschen Text für jedes Bigramm gezählt wurde, wie häufig es in diesem Text vorkommt. Leerzeichen und Satzzeichen wurden zuvor entfernt. Teilt man jetzt die Häufigkeiten für jedes Bigramm durch die Anzahl aller betrachteten Bigramme des langen Textes, erhält man pro Bigramm die Wahrscheinlichkeit, mit der dieses Bigramm in einem deutschen Text auftritt.
Um jetzt die Wahrscheinlichkeit zu berechnen, dass es sich bei einer gegebenen Buchstabenfolge um einen deutschen Text handelt, werden die Einzelwahrscheinlichkeiten aller in der Buchstabenfolge vorkommender Bigramme miteinander multipliziert. Je größer der errechnete Wert ist, desto wahrscheinlicher handelt es sich um einen deutschen Text.
Nun ist allerdings die Multiplikation eine für unsere Zwecke ungeeignete Operation. Erstens kostet sie Rechnerleistung, zweitens stößt man schnell an die Grenze des darstellbaren Zahlenbereichs, denn wenn der Klartext eine Länge von 1000 Zeichen hat, wären 999 Multiplikationen notwendig.
Wir greifen daher auf die Technik des Rechenschiebers zurück, und durch die Verwendung von Logarithmen wird die Multiplikation auf eine Addition zurückgeführt.
Es gilt:
log(a*b) = log(a) + log(b)
Es ist also vorteilhaft, pro Bigramm nicht seine Wahrscheinlichkeit abzulegen, sondern den Logarithmus seiner Wahrscheinlichkeit. Die Bewertung eines Textes reduziert sich damit auf die Aufsummierung dieser Log-Wahrscheinlichkeiten pro Bigramm. Diesen Wert werden wir als "Fitness" bezeichnen.
Die Exponentialfunktion als Umkehr zum Logarithmus muss nicht auf den Fitnesswert angewandt werden, da immer zwei Fitnesswerte miteinander verglichen werden. Die Logarithmusfunktion ist nämlich streng monoton steigend, und damit gilt:
Wenn a > b, dann log(a) > log(b)
Das ganze Verfahren ist auch exzellent auf der Seite Quadgram Statistics as a Fitness Measure beschrieben.
Die Implementierung wird ein zweidimensionales Array verwenden, das schon die Logarithmen der Bigramm-Häufigkeiten enthält. Zusätzlich wird dieses Array so normiert, dass es nur Integer-Werte enthält. Das Bigramm mit der geringsten Wahrscheinlichkeit erhält den Wert 0, das mit der größten Wahrscheinlichkeit den Wert 1000000.
Das verwendete normierte zweidimensionale Bigramm-Log-Array für die deutsche Sprache (puh, was für ein Sprachkonstrukt) sieht in PHP folgendermaßen aus:
$bigram_log = array(
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
array( 667643, 814073, 796829, 736398, 900826, 741569, 813861, 788369, 699600, 479374, 707898, 857087, 815163, 897533, 490330, 676425, 422461, 846932, 857860, 832287, 884117, 631007, 589078, 567159, 603432, 636022 ), # A
array( 777627, 566742, 455760, 585510, 904778, 513938, 613313, 551837, 761977, 497757, 496479, 709159, 534513, 586196, 692349, 448749, 201821, 733462, 696908, 665727, 745626, 500928, 572613, 196748, 497496, 540710 ), # B
array( 639470, 469604, 478356, 567519, 641395, 400968, 396361, 956682, 567258, 275114, 761165, 563847, 443642, 408262, 660573, 404478, 301372, 542887, 539392, 512206, 533574, 397361, 400681, 187510, 394527, 414007 ), # C
array( 869388, 658952, 556195, 732676, 954903, 643796, 648079, 637725, 876848, 545451, 628713, 669237, 652745, 643902, 726667, 635552, 486556, 723051, 729192, 669721, 755724, 636470, 663480, 280373, 525881, 611698 ), # D
array( 794468, 834762, 793766, 834116, 777830, 797294, 833736, 848495, 943814, 627477, 771549, 870848, 847761, 992329, 668097, 733691, 534822,1000000, 913042, 853289, 829528, 744365, 773572, 653522, 551680, 735569 ), # E
array( 775704, 592863, 542422, 720388, 797841, 728581, 643528, 570420, 733041, 507957, 548159, 685007, 605588, 593724, 732198, 575508, 287566, 752531, 665169, 769153, 792556, 543838, 569812, 325837, 343749, 563245 ), # F
array( 779078, 631468, 451025, 708584, 920639, 612285, 640288, 630280, 755968, 490286, 616500, 718737, 634707, 661945, 637054, 525428, 279907, 756405, 763964, 770546, 733842, 645096, 619364, 219225, 476882, 620891 ), # G
array( 862816, 661066, 482502, 745934, 884484, 630760, 646198, 629361, 779036, 532405, 641381, 777832, 742654, 766667, 767830, 555333, 337879, 829860, 739639, 834397, 739517, 633799, 719686, 173123, 507825, 627675 ), # H
array( 712112, 696745, 876239, 760088, 922084, 680889, 821359, 714292, 588591, 531371, 717294, 796529, 799943, 932820, 766462, 639064, 436183, 780013, 867853, 877370, 624190, 699579, 585670, 499103, 341852, 675620 ), # I
array( 742890, 251490, 243696, 270417, 692209, 206401, 221448, 348002, 422935, 196269, 328101, 249218, 308740, 278650, 603179, 331132, 20001, 299074, 324653, 219647, 667750, 277501, 235838, 30559, 103954, 156091 ), # J
array( 778465, 551793, 440606, 577622, 790952, 554655, 582218, 554763, 690191, 371392, 542734, 726545, 548164, 600503, 792600, 506502, 306922, 716439, 660686, 773508, 737251, 525637, 567381, 170315, 448582, 544030 ), # K
array( 838385, 703133, 600101, 752304, 868945, 676104, 686855, 601282, 854761, 486971, 644706, 841260, 658594, 661116, 738682, 588483, 353149, 579201, 780952, 800671, 752839, 631943, 615809, 242572, 583770, 631132 ), # L
array( 827980, 706498, 539812, 703094, 844747, 668446, 663389, 630557, 836771, 617245, 642624, 637455, 782438, 641362, 741333, 711729, 404326, 625044, 743132, 708702, 747750, 656059, 653923, 333242, 449381, 615044 ), # M
array( 857925, 782867, 680515, 931161, 905887, 774508, 882520, 755111, 845428, 674564, 801143, 730866, 772285, 831964, 765487, 716330, 529084, 708212, 867018, 858046, 807613, 753660, 785627, 376195, 518798, 790747 ), # N
array( 624141, 715479, 753636, 714931, 842480, 706935, 694698, 699480, 582759, 559553, 638508, 798487, 761887, 858806, 616833, 700978, 312146, 836899, 758194, 722234, 645652, 621737, 661692, 496755, 478661, 681482 ), # O
array( 749009, 434854, 469908, 575361, 738569, 680950, 438335, 615568, 727016, 319718, 482524, 693641, 469201, 412581, 722400, 669311, 182595, 790116, 583068, 651504, 665239, 443752, 425443, 197224, 379876, 455728 ), # P
array( 321589, 194224, 328556, 183285, 208304, 204963, 232257, 151321, 335839, 0, 152542, 245797, 254882, 164654, 164801, 146972, 94370, 161654, 278333, 194912, 641310, 218016, 225898, 32327, 34054, 165966 ), # Q
array( 872927, 794831, 717186, 860048, 900403, 770517, 800489, 761895, 848581, 672139, 792185, 767277, 777589, 809096, 820016, 714290, 478128, 736190, 850213, 846613, 828888, 739103, 765865, 380070, 538966, 756974 ), # R
array( 822843, 742931, 873615, 767171, 886042, 705123, 748535, 726908, 854909, 626724, 722322, 714765, 726355, 686650, 799094, 795872, 471862, 680969, 881732, 908332, 751825, 717405, 731757, 363267, 586967, 704174 ), # S
array( 852685, 712713, 572808, 800617, 943536, 688130, 721584, 743002, 848218, 605095, 665677, 735083, 725953, 707312, 765090, 645466, 398549, 805778, 835295, 792868, 800838, 704687, 773387, 368747, 548607, 799100 ), # T
array( 663090, 687564, 778458, 677780, 918864, 812528, 713101, 662421, 592514, 438689, 651662, 709191, 790503, 902196, 537047, 663551, 265326, 822415, 841124, 790577, 560582, 609214, 584222, 464725, 375036, 584501 ), # U
array( 638365, 453286, 348461, 472298, 824032, 490423, 455508, 414827, 715956, 323259, 410033, 400558, 426515, 383275, 823000, 421347, 138482, 434295, 488513, 401835, 446704, 404780, 482349, 188156, 279813, 396924 ), # V
array( 799874, 433610, 398448, 457814, 838498, 433480, 419952, 455710, 820315, 449847, 435166, 435535, 510486, 479987, 741829, 426787, 102948, 468587, 539647, 412810, 712349, 387621, 488148, 207235, 453104, 365366 ), # W
array( 496801, 422333, 372761, 457712, 522562, 427088, 413256, 402382, 547756, 231842, 433476, 385389, 419207, 382104, 384083, 566629, 127935, 342566, 473548, 531044, 464196, 415437, 387963, 397297, 311212, 389403 ), # X
array( 548740, 482744, 486355, 487231, 588069, 407851, 440799, 433129, 473732, 306466, 442851, 484946, 550134, 499402, 523018, 521949, 154253, 459292, 624622, 477862, 452986, 414584, 447193, 216276, 254137, 385133 ), # Y
array( 675889, 575025, 401521, 586244, 809478, 529852, 548817, 507297, 734082, 367971, 536599, 596396, 545677, 502678, 606005, 482719, 216276, 462571, 571182, 704012, 826072, 558518, 706228, 171799, 450969, 534116 ) # Z
);Der Index 0 entspricht dem "a", 1 dem "b", usw. Die erste Dimension des Arrays entspricht dem ersten Buchstaben eines Bigramms, die zweite Dimension entsprechend dem zweiten Buchstaben. Das Bigramm "ab" hat demnach den Fitnesswert 814073.
Zwei Hinweise noch, was bei der Erstellung dieses Arrays beachtet werden muss:
- Die original-Datei enthält auch Bigramme mit Umlauten und "ß". Da bei einer Vigenère Verschlüsselung "ß" als "ss", "ä" als "ae", usw. geschrieben wird, wird folgendes Verfahren angewendet: Zum Beispiel wird das Bigramm "äu" (373946) erweitert zu "aeu". Dies wiederum entspricht den zwei Bigrammen "ae" und "eu". Der Wert 373946 wird also zu den Werten der Bigramme "ae" und "eu" aufaddiert.
- Sollte ein Bigramm die Häufigkeit 0 haben, so wird sie zu 1 erhöht, weil wir ja den Logarithmus bilden müssen, und log(0) ja bekanntlich minus Unendlich ist.
Zur Verdeutlichung hier jetzt ein Beispiel, welches das oben dargestellte Array verwendet:
Der Text "hallo" führt zu folgendem Fitnesswert:
| Bigramm | Fitness |
|---|---|
| ha | 862816 |
| al | 857087 |
| ll | 841260 |
| lo | 738682 |
| Gesamt | 3299845 |
Und der Text "kjexg" ergibt:
| Bigramm | Fitness |
|---|---|
| kj | 371392 |
| je | 692209 |
| ex | 653522 |
| xg | 413256 |
| Gesamt | 2130379 |
Das Wort "hallo" hat eine größere Fitness und kommt damit der deutschen Sprache näher als "kjexg".
Soweit das Prinzip.
Im folgenden wird es jedoch gar nicht nötig sein, für jeden Schlüsselkandidaten die Fitness des kompletten Klartextes zu berechnen.
Der Algorithmus
Nehmen wir folgenden Vigenère-Cipher als Beispiel:
aorqohpeicsblloimecdultvhj
Die Schlüssellänge beträgt 5. Der Ciphertext wird zur besseren Darstellung alle 5 Zeichen umgebrochen. Alle untereinander stehenden Buchstaben werden durch den selben Buchstaben des Schlüssels dekodiert. Jede Spalte entspricht also einer Gruppe. Gruppe 0 enthält also die Buchstaben a, h, s, i, u, j.
01234 ;Index
aorqo ;Ciphertext
hpeic
sbllo
imecd
ultvh
jJetzt wird vom Schlüssel nur der Index 0 und Index 1 betrachtet (also die Nachbarn Gruppe 0 und Gruppe 1). Angenommen, der Schlüssel wäre dort "aa", wie würde sich dieser Teil des Schlüssels auf die entsprechenden Bigramme des resultierenden Klartextes auswirken? Das Bigramm "aa" im Schlüssel würde zu folgenden Bigrammen des Klartextes führen: "ao", "hp", "sb", "im", "ul" (in diesem Fall sind es genau die Bigramme des Ciphertextes, da für den Buchstaben "a" im Schlüssel Cipherbuchstabe und Klartextbuchstabe identisch sind). Also bilden wir den Fitnesswert von diesen 5 Bigrammen und merken uns "aa" zunächst als bestmöglichen Schlüssel. Den Rest des Schlüssels, des Ciphertextes oder des Klartextes betrachten wir nicht, denn darauf hat weder der Index 0 noch der Index 1 des Schlüssels einen Einfluss.
Nun führen wir das ganze mit dem nächsten Bigramm "ab" durch. Falls hier die Bigramme des resultierenden Klartextes zu einem höheren Fitnesswert führen als der von "aa", so merken wir uns "ab" und den entsprechenden Fitnesswert als bestes Bigramm.
Das wird wiederholt für alle 26*26 = 676 möglichen Bigramme. Den besten Fitnesswert (4314768) erreicht das Bigramm "qu":
01234 ;Index qu ;Schlüssel kurqo ;Ciphertext bzw. resultierender Klartext rveic chllo ssecd ertvh t
Das Bigram "qu" im Schlüssel führt zu den Bigrammen "ku" (737251), "rv" (739103), "ch" (956682), "ss" (881732) und "er" (1000000) im Klartext. Das letzte einzelne "t" wird nicht berücksichtigt.
Fitness für das Schlüsselbigramm "qu": 737251 + 739103 + 956682 + 881732 + 1000000 = 4314768 Nachdem also das beste Bigramm des Schlüssels für den Index 0 und 1 identifiziert wurde, wird die nächste Bigramm-Position im Schlüssel untersucht, also Index 1 und 2. So wird fortgefahren, bis das Ende des Schlüssels erreicht wurde. Als letztes wird auch das Bigramm mit dem Schlüsselindex 4 und 0 betrachtet, denn dieses beiden Stellen im Schlüssel führen ja auch zu Bigrammen im Klartext, eben in der Darstellung oben nur getrennt durch einen Zeilenumbruch.
Es ergibt sich folgende Tabelle:
| Key-Idx | Fitness | Bigramm |
|---|---|---|
| 0,1 | 4314768 | qu |
| 1,2 | 4156934 | ua |
| 2,3 | 4324197 | ar |
| 3,4 | 4051773 | ib |
| 4,0 | 4261237 | kq |
Für jede Position im Schlüssel haben wir jetzt einmal das Bigramm mit dem Zeichen im Schlüssel davor und danach betrachtet, es gibt jetzt also für jede Position im Schlüssel zwei Kandidatenzeilen aus obiger Tabelle. Es wird einfach die Zeile mit dem höheren Fitnesswert verwendet.
Beispiel: Index = 2 wird abgedeckt durch Key-Idx(1,2) und Key-Idx(2,3). Da Key-Idx(2,3) den höheren Fitnesswert hat, wird das "a" aus dem Bigramm "ar" verwendet (andernfalls wäre das "a" aus dem Bigramm "ua" verwendet worden).
Es ist zu beobachten, dass das Bigramm "ib" daher nicht verwendet wird, und das ist auch gut so für dieses Beispiel. Die verwendeten Buchstaben für den Schlüssel sind in der Tabelle oben farblich hinterlegt.
Es ergibt sich also der Schlüssel quark. Der daraus resultierende Klartext lautet kurzerverschluesseltertext.
Dieses Verfahren lässt sich ohne Einschränkungen genauso gut auf die Beaufort-Variante sowie die Autokey-Vigenère-Variante anwenden.
Die richtige Schlüssellänge bestimmen
Bisher wurde nur der Fall betrachtet, dass die korrekte Schlüssellänge bekannt ist. Und es wurde ja schon darauf hingewiesen, dass eine Autokorrelation unbrauchbare Aussagen liefern kann.
Die hier verwendete Lösung liegt darin, einfach alle Schlüssellängen mit dem beschrieben Algorithmus durch zu probieren, um letztlich den Schlüssel zu wählen, dessen Klartext den größten Fitnesswert erreicht.
Das wird möglich, weil der Algorithmus recht performant ist.
Beispiel: Der Klartext "Das wird moeglich, weil der Algorithmus recht performant ist." wird mit dem Wort "blaise" verschlüsselt. Wir erhalten:
elseavexomypjnhewmmoezsphzrqllnfszwgiepmjjpcmifxjdt
Weder eine Autokorrelation noch der Friedman-Test (-8.003) zu diesem Ciphertext führen auf die Spur zur richtigen Schlüssellänge:
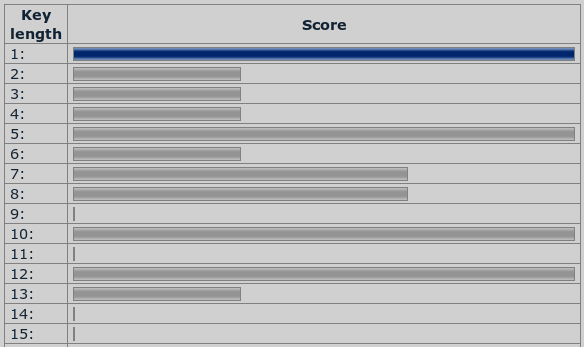
Autokorrelation für einen Vigenère-Cipher mit Schlüssellänge 6
Anders sieht es aus, wenn für jede mögliche Länge des Schlüssels die Fitness des besten Schlüssels genommen wird:
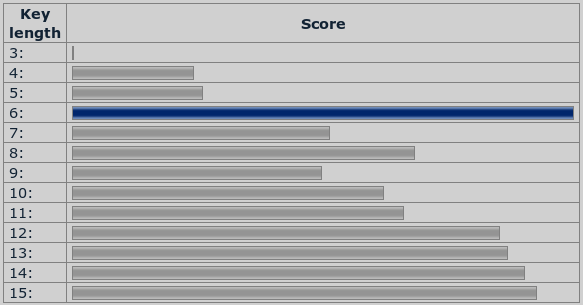
Derselbe Vigenère-Cipher, Schlüssellänge über die Fitness bestimmt
Bei dem Diagramm fällt auf, dass es mit größerer Schlüssellänge eine Tendenz zu einem höheren Fitnesswert gibt. Das ist leicht erklärbar, denn je länger der Schlüssel wird, desto weniger Buchstaben werden mit demselben Zeichen des Schlüssels kodiert. Im Extremfall ist der Schlüssel genauso lang wie der Ciphertext. Klar, dass in diesem Fall jeder Schlüsselbuchstabe so gewählt werden kann, dass sich ein optimaler Klartext und damit ein hoher Fitnesswert ergibt. Es gilt also, die Aufmerksamkeit besonders auf markante Ausreißer zu richten, und nicht blind den höchsten Fitnesswert zur Bestimmung der Schlüssellänge heranzuziehen.
Die Schlüssellänge über die Fitness zu bestimmen hat übrigens noch einen anderen Vorteil: Das Verfahren lässt sich ohne Einschränkungen genauso gut für die Autokey-Variante anwenden. Die oft zu findende Aussage, die Kryptoanalyse von Autokey-Vigenère Kodierungen ist aufwändiger als für die klassische Vigenère-Variante, muss meiner Meinung nach relativiert werden, steht heutzutage doch genügend Rechenleistung zur Verfügung, um auf eine Autokorrelation und den Friedman-Test vollständig verzichten zu können.
Die Implementierung
Das Herzstück der Implementierung sieht in PHP folgendermaßen aus:
function break_vigenere ($cipher_text, $key_len) {
global $vigenere_square, $bigram_log;
$key = array();
for ($key_idx = 0; $key_idx < $key_len; $key_idx++) {
$best_fitness = 0;
for ($key_ch1 = 0; $key_ch1 < 26; $key_ch1++) {
for ($key_ch2 = 0; $key_ch2 < 26; $key_ch2++) {
$fitness = 0;
for ($text_idx = $key_idx; $text_idx < (count($cipher_text) - 1); $text_idx += $key_len) {
$clear_ch1 = $vigenere_square[$cipher_text[$text_idx ]][$key_ch1];
$clear_ch2 = $vigenere_square[$cipher_text[$text_idx+1]][$key_ch2];
$fitness += $bigram_log[$clear_ch1][$clear_ch2];
}
if ($fitness > $best_fitness) {
$best_fitness = $fitness;
$best_key_ch1 = $key_ch1;
$best_key_ch2 = $key_ch2;
}
}
}
if ($key_idx == 0) {
$best_score_0 = $best_fitness;
$best_key_ch1_0 = $best_key_ch1;
$best_key_ch2_0 = $best_key_ch2;
array_push($key, 0); # just a placeholder
}
else {
array_push($key, ($prev_best_score > $best_fitness) ? $prev_best_key_ch2 : $best_key_ch1);
}
$prev_best_score = $best_fitness;
$prev_best_key_ch2 = $best_key_ch2;
}
$key[0] = ($best_fitness > $best_score_0) ? $best_key_ch2 : $best_key_ch1_0 ;
return $key;
}Die Funktion break_vigenere berechnet zu einem gegebenen Ciphertext und einer vorgegebenen Schlüssellänge den besten Schlüssel.
Der Ciphertext ($cipher_text) wird als Array aus Integer-Werten der Funktion übergeben. Dabei wird das "a" durch eine 0 repräsentiert, das "b" durch 1, usw. Alle Leerzeichen, Satzzeichen und sonstige Sonderzeichen wurden vorher entfernt, und zwischen Groß- und Kleinbuchstaben wird nicht unterschieden. Jedes Array-Element befindet sich also in dem Bereich 0..25.
Auch für das Array $key wird dieselbe Repräsentation der Buchstaben verwendet ("a"=0, "b"=1, usw).
Das Array $bigram_log wurde oben schon erklärt. Bleibt noch das zweidimensionale Array $vigenere_square. Über dieses Array findet die Dekodierung eines Buchstabens statt. Der erste Index entspricht dem Buchstaben (Bereich: 0..25) des Ciphertextes, der zweite Index dem Buchstaben (Bereich: 0..25) des Schlüssels. Ausgelesen aus dem Array wird der entsprechende Buchstabe (Bereich: 0..25) des Klartextes. Die Verwendung eines Arrays wurde gewählt, weil damit dieser Code unverändert für die Beaufort-Variante funktioniert: lediglich der Inhalt muss vorher entsprechend des Beaufort-Quadrats aufgesetzt werden.
Zeile 4 enthält die Schleife, um über jede benachbarte Bigrammgruppe im Schlüssel zu iterieren.
Die Zeilen 6 und 7 definieren die Schleifen, um alle 676 möglichen Bigramme pro Schlüsselposition auszuprobieren.
Die innerste Schleife in Zeile 9 iteriert für jeden der 676 Bigramm-Kanditaten über den Ciphertext und ermittelt so die entsprechende Fitness.
Key-Index 0 erhält noch eine Sonderbehandlung (Zeile 21), da hier der optimale Buchstabe des Schlüssels erst bestimmt werden kann, wenn auch die letzte Stelle im Schlüssel bearbeitet wurde. Deshalb wird erst mit Zeile 33 der Buchstabe an dieser Schlüsselposition bestimmt.
Für das Lösen von Autokey-Ciphern muss die Implementierung leicht angepasst werden, da die Regeln zur Dekodierung entsprechend berücksichtigt werden müssen.
Die vorgestellt Implementierung ist als Online-Version unter diesem Link verfügbar.
Die Eingabe der Schlüssellänge kann als Bereich erfolgen. Die maximale Schlüssellänge unterliegt nur einer Einschränkung: sie darf nicht größer sein als die Ciphertextlänge.
Alle Schlüssellängen werden durchprobiert, und zu jeder Schlüssellänge ist der Schlüssel selber sowie der entsprechende Fitnesswert als Statistik bzw. als Histogramm abrufbar. Der Fitnesswert wurde noch durch die Anzahl der Bigramme pro Ciphertext geteilt (und durch 10000, wegen der besseren "Lesbarkeit"), um so auch einen Vergleich zwischen unterschiedlich langen Texten zu erlauben. Dadurch wird eine große Flexibilität erreicht, und es wird recht einfach, auch "schwierige" Vigenère-Ciphers zu lösen.
Erfahrungen zeigen, dass typisch deutsche Texte einen Fitnesswert um 80.0 oder höher liefern. Zufallstexte liegen dagegen bei einem Fitnesswert von ca. 50.0.
Die Implementierung bietet auch eine Autokorrelation an, aber mir ist kein Vigenère-Cipher bekannt, für den sie bessere Ergebnisse liefert als eine Bewertung über die Fitness.
Ergebnis
Die vorgestellte Implementierung basierend auf Bigrammen liefert durchweg bessere Ergebnisse, als vergleichbare Vigenère-Solver, die mit Monogrammen arbeiten. So ist es möglich, auch kurze Vigenère-Cipher mit relativ langen Schlüsseln zu lösen.
Für den Vigenère-Solver auf dieser Seite wurden gegenüber dem vorgestellten Code zusätzliche Verbesserungen implementiert. Neben Laufzeitoptimierungen wurden weitere Algorithmen kodiert, die zur Bestimmung von noch besseren Schlüsseln führen. Dafür kommen unter anderem Trigramme zum Einsatz. Selbst bei einem Verhältnis Schlüssellänge:Textlänge = 1:4 liefert der Solver noch brauchbare, oftmals sogar vollständig richtige Ergebnisse.
Hier nun ein herausforderndes Beispiel, das mit dem Solver gelöst werden kann:
VVRQI EREOY LDPTT MWNFL ECKAV MZPWE EHRZK UHXHI KCISC BGBZH LHEPK DSERK AEESJ KOLIF ZJKHB SXSZK SALUA ZPGVX EOKIX OZEIQ VHBHF HWFJI MITSP XHCZS JTYWH VTRSW KVMSG QTKSY WYMOF XQPSH IGSOH GMVXC ITPKW YZXAH JVRSK ZWGXT RMTXW AGFDV IQGTK SVXEM OMFWN OFOR
Achtung, die Schlüssellänge ist groß, aber sie ist kleiner als 100.
Andere Online Vigenère-Solver
Hier jetzt noch eine Auflistung von anderen Online Vigenère-Solvern.
http://www.mygeocachingprofile.com/codebreaker.vigenerecipher.aspx
Offensichtlich nur für englische Vigenère-Cipher. Soll optimiert sein für "Geocaching-Texte". In der Ausgabe wird man erschlagen von Lösungsvorschlägen.
http://www.dcode.fr/vigenere-cipher
Eine Seite, die sich mit vielen unterschiedlichen Verschlüsselungen beschäftigt. Beim Brechen von Vigenère-Ciphern kann man die Sprache nicht vorgeben, und auch hier werden sehr viele mögliche Lösungen angeboten.
http://www.geocachingtoolbox.com/index.php?lang=en&page=vigenereCipherSolve
Unterstützt die gängigsten Sprachen, maximale Schlüssellänge ist 50.
http://www.sichere.it/vigenere_tool.php?language=DE
Ein Vigenère-Solver mit einem anderen und interessanten Konzept. Zur Lösung werden Wörterbücher herangezogen. Entwickelt für extrem kurze Vigenère-Ciphers. Schlüssel und Klartext müssen Wörter aus dem Wörterbuch enthalten.